Largest Rectangle in Histogram

24% Accepted

Given n non-negative integers representing the histogram's bar height
where the width of each bar is 1, find the area of largest rectangle in the histogram.

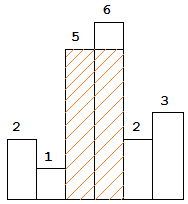
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example
Given height = [2,1,5,6,2,3],
return 10.

Tags Expand

• Array
• Stack

暴力O(n2)不会通过的方法

public class Solution {
    /**
     * @param height: A list of integer
     * @return: The area of largest rectangle in the histogram
     */
    public int largestRectangleArea(int[] height) {
        // write your code here
        int maxarea = 0;
        for (int i = 0; i < height.length; i++) {
            int min = Integer.MAX_VALUE;
            for (int j = i; j >= 0; j--) {
                min = Math.min(min, height[j]);
                maxarea = Math.max(min * (i - j + 1), maxarea);
            }
        }
        return maxarea;
    }
}

高级解法

• 思路来源
• 图画解释
• 单调栈，顾名思义就是说栈内的元素，按照某种方式排序下，必须是单调的。如果新入栈的元素破坏了单调性，就弹出栈内元素，直到满足单调性。它可以很方便地求出某个数的左边或者右边第一个比它大或者小的元素，而且总时间复杂度O(N)。
• 要想找到里面的最大的面积，一定会有这么一种情况，得出的矩形的高度一定为所包含的某一个高度一致的。所以我们可以对某一个柱子的高度为标准，尽量的向两头扩展，这样就可以找出以它高度为标准的，并包含它本身的最大矩形。然后对每一个柱子都做类似的工作，最后挑出里面最大的矩形
• 所以如果我们从第一个开始计算到第n个，计算到i时，如果我们可以快速的找出左边第一个（这里第一的意思是离i最近）的比i的高度小的，就可以完成了向左扩展的工作，而向右扩展，我们本来就是一直向右走，所以直接扩展。这时候就轮到：单调栈出场了！

#

如：2 1 4

第一个：2，以2为高度为准，向左右两头扩展，它只能想右扩展，因为1比2低了，就不可能扩展到1了。宽度只有1。

第二个：1，以1为高度为准，向左右两头扩展，向左，因为2比1高可以扩展过去；向右，因为4也高于1所以扩展到4，这样以1为高度的矩形宽为3了；

第三个：4，以4为高度为准，向左右两头扩展，向左，因为4比1、2都高，显然不可以扩展过去，这样以4为高度的矩形宽为1了。

所以要将其扩展过去，必须高度高于当前扩展点的高度。

所以如果我们从第一个开始计算到第n个，计算到i时，如果我们可以快速的找出左边第一个（这里第一的意思是离i最近）的比i的高度小的，就可以完成了向左扩展的工作，而向右扩展，我们本来就是一直向右走，所以直接扩展。这时候就轮到：单调栈出场了！

一直保持单调递增的栈。

思考刚才的例子：

2进栈，左边无比其小的元素，记录其最左扩展位置为1

1准备进栈，因为其进栈就破坏了单调栈的性质（2>1），这时2要出栈，因为1<2也说明了2不可能向右扩展，出栈，计算以2为准的矩形 2*1，然后1才进栈。1进栈前，发现其前一个元素，既是当前的栈顶2，比1高，而且2的左扩展从位置1开始，所以1也有理由从2的左起始位置开始（注意：2比1高），所以2出栈后，1进栈，其左扩展应为2的左扩展位置1；

4准备进栈，因为4>1直接进栈，其左扩展位置只能为3了。

最后要清空栈：4退栈，以为是最右的了，这此时右扩展只能为3了。左右扩展都为3，即是其本身，矩形为4*1；记录其位置以备后需；

1退栈，最右扩展只能是上一个退栈的元素位置，因为其高度比1高（单调栈的性质），所以利用刚才记录的位置，1的左右扩展就为1，3了，矩形1*3；

完成。

改进后的算法，debug了一个半小时

• 重写 : 再重写
• stack push进去的是index，因为再找边界的时候找的是下标i, value的值可以直接height[i]
• 在最后已经遍历完，栈底只剩下一个数时候，强行进入pop阶段而不是push，所以用了int cur = (i == height.length) ? -1 : height[i];
• 非常巧妙的办法
• 找左右比该节点大的数用递减栈，找左右比该节点小的数用递增栈

public class Solution {

    public int largestRectangleArea(int[] height) {
        // write your code here
        if (height == null || height.length == 0) {
            return 0;
        }
        Stack<Integer> stack = new Stack<Integer>();
        stack.push(0);
        int maxArea = 0;
        int i = 1;
        //for (int i = 1; i <= height.length;)
        //本来写的for循环，更好理解
        //优化改为while
        while (i <= height.length) {
            /*
            -1是为了把之前的全部pop出来
             */
            int cur = (i == height.length) ? -1 : height[i];
            if (stack.isEmpty() || cur >= height[stack.peek()]) {
                stack.push(i);
                i++;
            } else {
                int thisIndex = stack.pop();
                int thisHeight = height[thisIndex];
                int startIndex;
                //考虑到pop后的边界情况
                if (!stack.isEmpty()) {
                    startIndex = stack.peek();
                } else {
                    startIndex = -1;
                }
                /*
                i代表了还没pop的时候，递增栈中右边最大的index
                 */
                maxArea = Math.max(maxArea, thisHeight * (i - startIndex - 1));
            }
        }
        return maxArea;
    }
}

别人的简洁代码

public int largestRectangleArea2(int[] height) {
        Stack<Integer> stack = new Stack<Integer>();
        int i = 0;
        int maxArea = 0;
        int[] h = new int[height.length + 1];
        h = Arrays.copyOf(height, height.length + 1);
        while(i < h.length){
            if(stack.isEmpty() || h[stack.peek()] <= h[i]){
                stack.push(i++);
            }else {
                int t = stack.pop();
                //减1是因为这个高点已经被pop了,此时stack.peek()是下一个点的index
                //而且这里不能是i - t,必须是i - stack.peek() - 1, 因为找的是左边最小值
                maxArea = Math.max(maxArea, h[t] * (stack.isEmpty() ? i : i - stack.peek() - 1));
            }
        }
        return maxArea;
    }